Geometría con ggplot

ggplot es el estándar para visualización de datos en R. Siempre quise explorar si podía servir para hacer diagramas más conceptuales. En este post uso ggplot para dibujar algunas formas geométricas.

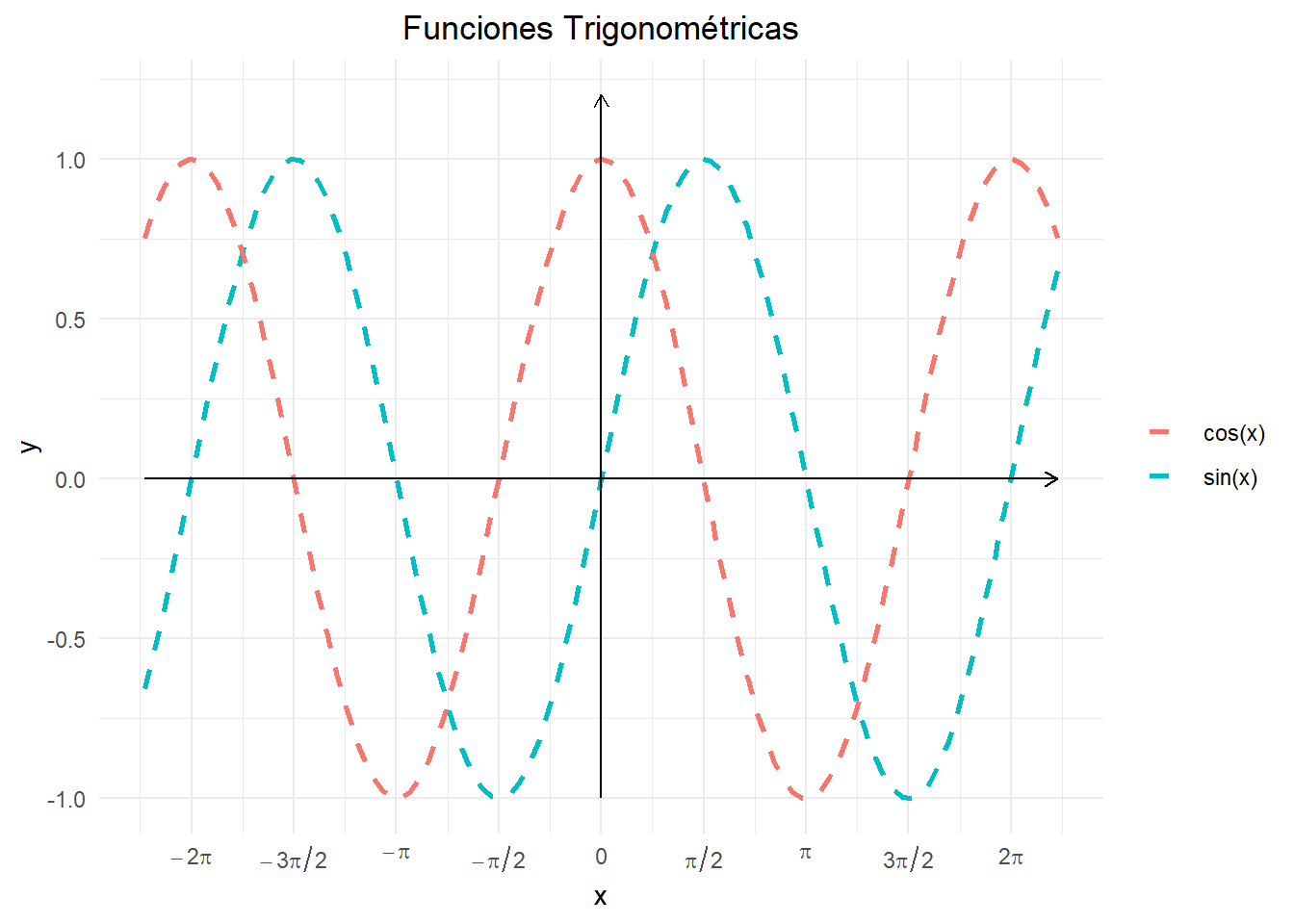
Para dibujar el gráfico de una función, podemos usar stat_function. En el primer gráfico, dibujo $sin(x)$ y $cos(x)$. Especifico aes(colour = "sin(x)") para que el color de ese cada geom quede ligado al texto correcto en la leyenda.

geom_segment y scale_x_continuous permiten especificar la posición y etiqueta de las guías.

Este post de stackoverflow sobre como poner letras griegas en ggplot explica como poner caractéres del alfabeto griego en los ejes usando expression().

library(tidyverse)
library(ggplot2)
theme_set(theme_minimal())

# Crear etiquetas para eje x
lbls <- c( expression(-2 * pi),
           expression(-3 * pi / 2),
           expression(- pi),
           expression(-pi/2),
           0,
           expression(pi/ 2),
           expression(pi),
           expression(3 * pi /2),
           expression(2 * pi)
           )


# Gráfico
ggplot(data_frame(x = c(-7, 7)), aes(x = x)) +
  stat_function(fun = function(x) { sin(x) }, 
                geom = "line", 
                linetype = "dashed", 
                size = 1,
                aes(colour = "sin(x)")) +
  stat_function(fun = function(x) { cos(x) },
                linetype = "dashed",
                size = 1,
                aes(colour = "cos(x)")
                ) +
  scale_x_continuous(
    breaks = seq(-2 * pi, 2*pi, pi/2),
    labels = lbls
  ) + 
  labs(x = "x", y = "y") + 
  geom_segment(aes(x=-7, xend = 7, y=0, yend=0), 
               size = 0.5,
               arrow = arrow(length = unit(0.2, "cm"))) + 
  geom_segment(aes(x=0, xend=0, y=-1, yend=1.2),
               size = 0.5,
               lineend = "butt",
               arrow = arrow(length = unit(0.2, "cm"))) + 
  labs(title = "Funciones Trigonométricas") + 
  theme(
    plot.title = element_text(hjust = 0.5),
    legend.title = element_blank(),
  )

Círculo

stat_fun resuelve el problema de graficar funciones, pero no sirve cuando queremos graficar otro tipo de objeto. La ecuación de un círculo es

$$ (x-h)^2+(y-k)^2=r^2 $$

donde $(h, k)$ es el centro y $r$ el radio. Escribir esta ecuación explícitamente como una función puede resultar complicado.

Este post en Stack Overflow explica como graficar una función en forma paramétrica usando annotate.

library(ggplot2)
library(latex2exp)

center <- c(x=3, y=1)
#pt1 <- c(x=1, y=1)
#pt2 <- c(x=5, y=1)
pt3 <- c(x=3, y=3)
pt4 <- c(x=3, y=-1)
pts <- dplyr::bind_rows(center,pt3, pt4)
radius <- 2
t <- seq(0, 2*pi, length.out = 100)

g <- ggplot() + 
  geom_segment(aes(x=-1, xend = 6, y=0, yend=0),
               size = 0.5,
               arrow = arrow(length = unit(0.2, "cm"))) + # Eje X
  geom_segment(aes(x=0, xend=0, y=-1, yend=4),
               size = 0.5,
               lineend = "butt",
               arrow = arrow(length = unit(0.2, "cm"))) + # Eje Y
  annotate("path", 
           x = center[1] + radius * cos(t),
           y = center[2] + radius * sin(t)) + 
  geom_point(data = pts, aes(x=x, y =y)) + 
  geom_text(data = pts,
            parse = TRUE,
            nudge_y = 0.2,
            aes(x=x, y=y, label = paste0("list(", x ,",", y, ")"))) +
  annotate("point", x=1, y=1) + 
  annotate("text", x=1.25, y=1, label="1,1") + 
  annotate("point", x=5, y=1) + 
  annotate("text", x=4.75, y=1, label="5, 1") + 
  labs(x="", y="") + 
  ggtitle(TeX("(x-3)^2+(y-1)^2=4")) + 
  coord_fixed()
g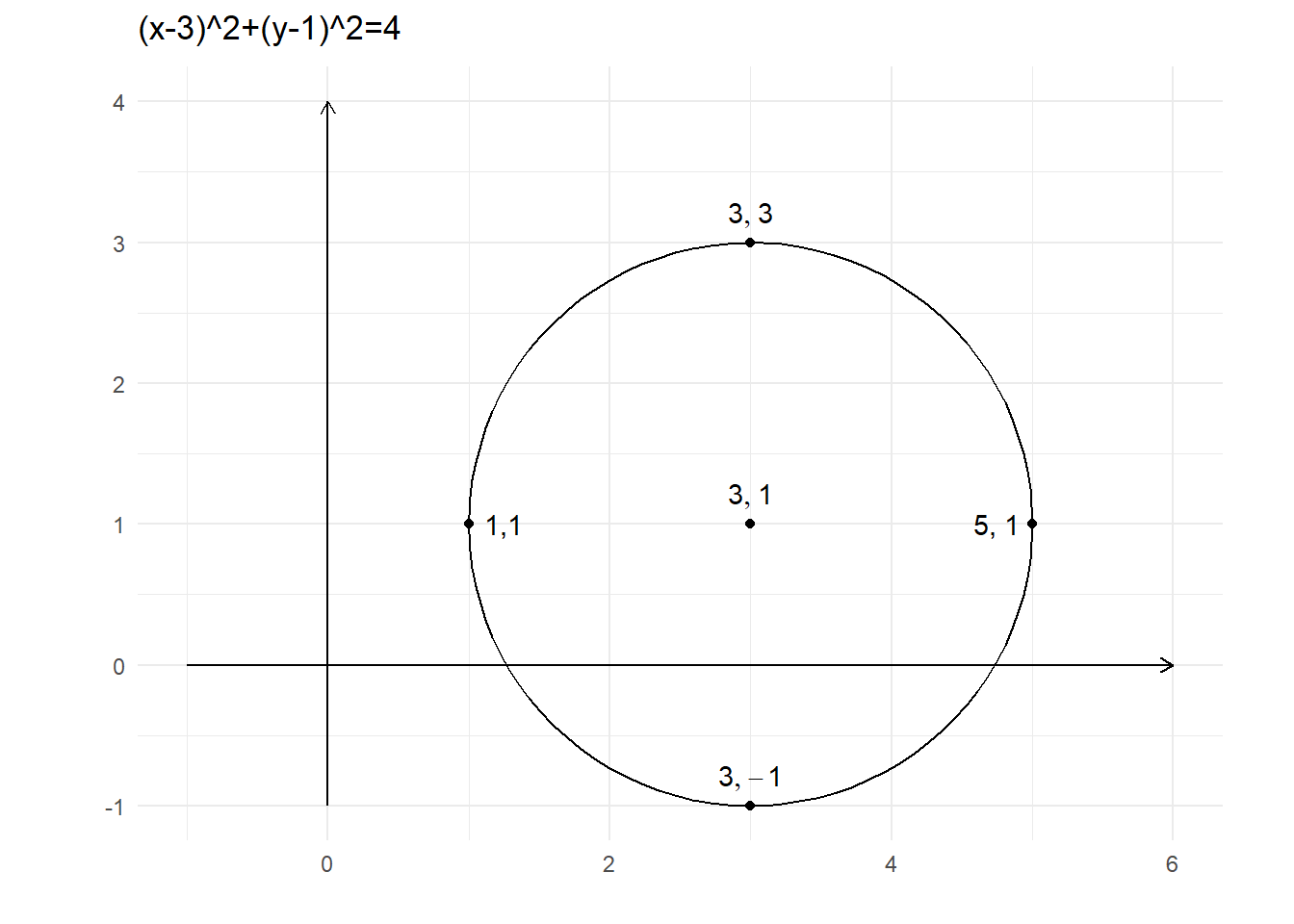

Parábola

Una parábola es un conjunto de puntos que equidista de una línea (directriz) y un punto (foco). Estos puntos satisfacen:

$(x-h)^2=4p(y-k),\, (p \neq 0)$

El vértice de la parábola está en $(h,k)$ y la directriz $y=k-p$. El foco está en $(h, k+p)$ si la parábola es abierta hacia arriba.

Ejemplo

$x^2=16y$ es una parábola con vértice en $(0,0)$, $p = 4$ y foco en $(0,4)$.

focus <- list(x=0, y=4, lab = "Foco")
vertex <- list(x=0, y=0, lab = "Vértice")
notable_points <- bind_rows(focus, 
                            vertex)
pt <- data_frame(x=5, y=round(5^2/16, 2))

p <- ggplot(data_frame(x=0), aes(x=x)) +
  geom_segment(aes(x=-9, xend = 9, y=0, yend=0),
               size = 0.5,
               arrow = arrow(length = unit(0.2, "cm"))) + # Eje X
  geom_segment(aes(x=0, xend=0, y=-5, yend=10),
               size = 0.5,
               lineend = "butt",
               arrow = arrow(length = unit(0.2, "cm"))) + # Eje Y
  stat_function(fun = function(x) { x^2 / 16}) + 
  xlim(-9, 9) + 
  ylim(-5, 10)

x <- 5

g_2 <- p +
  geom_point(data = notable_points, aes(x=x, y=y)) + 
  geom_text(data=notable_points, 
            size = 3,
            nudge_y = 1.25,
            nudge_x = 1.25,
            aes(label = paste0(lab, "\n(", x, ",", y, ")"), 
                x = x, y = y)) + 
  geom_hline(yintercept = -4, linetype = "dashed") + 
  annotate("text", x= 3, y= -3.3, label = "Directriz", size = 3) +
  ggtitle(TeX('$y=x^2/16$')) + 
  theme(
    plot.title = element_text(hjust = 0.5)
  ) + geom_point(data = pt, aes(x=x, y=y)) + 
  geom_segment(aes(x= focus$x, y=focus$y, xend=pt$x, yend=pt$y),
               linetype = "dashed") + 
  geom_segment(aes(x=pt$x, y=pt$y, xend=pt$x, yend = -4),
               linetype = "dashed") + 
  annotate("text", 
           label = "phantom(0) == phantom(0)", 
           parse = TRUE,
           angle = 60,
           size = 5,
           x = 2.5, y= 2.85) + 
  annotate("text", 
           label = "phantom(0) == phantom(0)", 
           parse = TRUE,
           size = 5,
           x = 5, y= -2)
g_2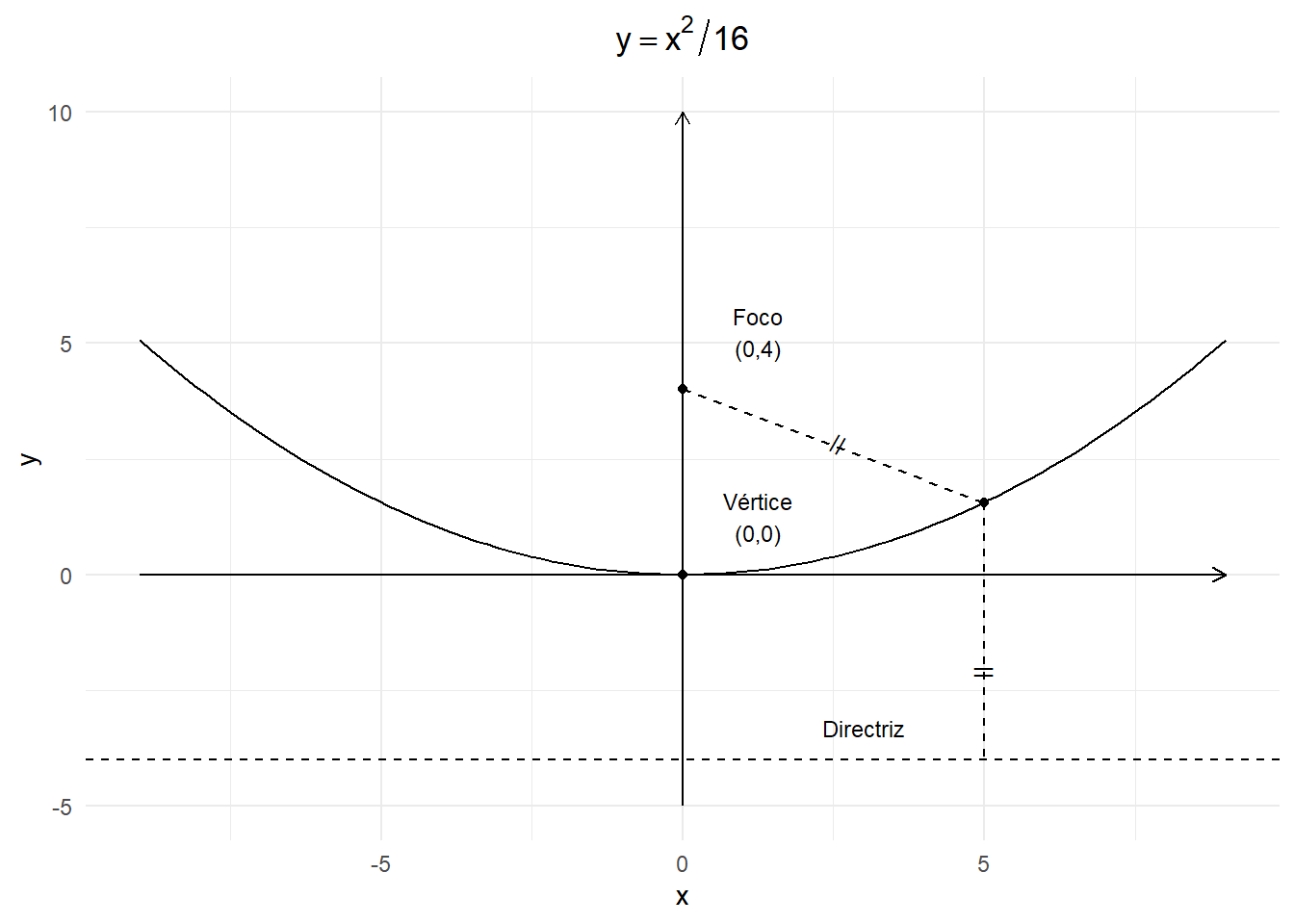

Todos los puntos de la parábola estan a la misma distancia del foco que de la directriz.

Una parábola con eje horziontal

Dibujar una parábola con eje vertical es simple porque podemos usar stat_fun. Pero si queremos dibujarlas con eje horizontal no podemos escibir los puntos de la parábola como un función y pasarsela a stat_function.

La ecuación $y^2+6y+8x+25 = 0$ no parece una parábola, pero si completamos el cuadrado:

\begin{align} y^2+6y+8x+25 &= 0\\ y^2+6y+9+8x+25-9 &= 0\\ (y+3)^2 &= -16-8x\\ (y+3)^2 &= 4(-2)(x+2) \end{align}

Es una parábola con vértice $(-2, -3)$, p es $-2$, el foco $(-4,-3)$ la directriz es $x=0$.

Pero como la orientación de esta parábola es horizontal, no es una función. Cómo la graficamos con ggplot?

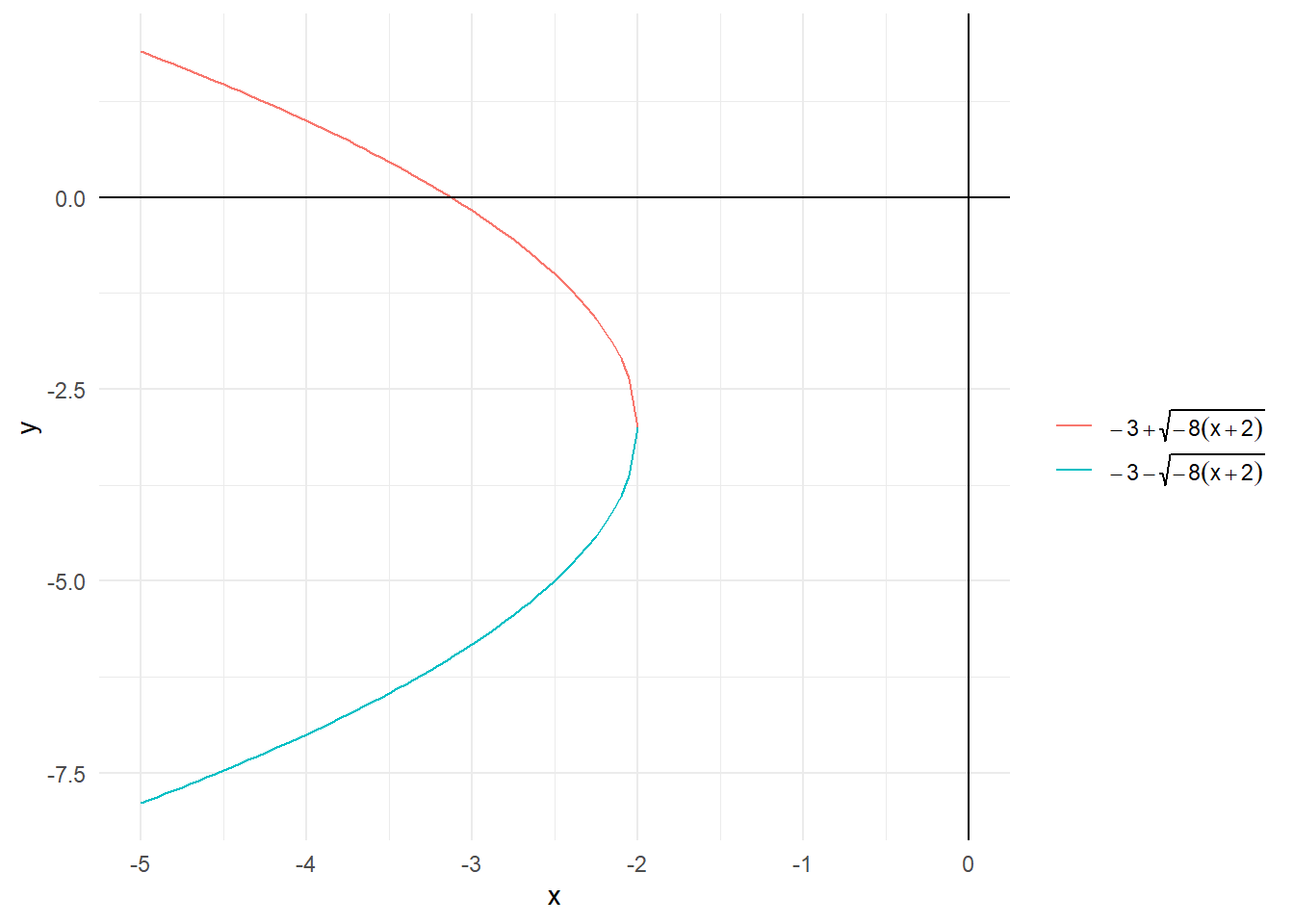
Si despejamos $y$ en función de $x$, obtenemos dos funciones: \begin{align} (y+3)^2 &= (-8)(x+2)\\ y &= -3 \pm \sqrt{-8(x+2)}\\ y_1 &=-3 + \sqrt{-8(x+2)}\\ y_2 &=-3 - \sqrt{-8(x+2)}\\ \end{align}

Podemos graficar $y1$ y $y2$:

x <- seq(-5, 0, length.out=1e3)
lbs <- list(bquote(-3 + sqrt(-8*(x+2))), # investigar bquote!
            bquote(-3 - sqrt(-8*(x+2))))

g_3 <- ggplot(data_frame(x=x), 
            aes(x=x, color = color)) + 
  stat_function(data = data_frame(x=x, color = factor(1)),
                fun = function(x) { -3 + sqrt(-8*(x+2)) }) + 
  stat_function(data = data_frame(x=x, color = factor(2)),
                fun = function(x) { -3 - sqrt(-8*(x+2)) }) + 
  scale_color_manual(labels = lbs,
                     name = "",
                     values = c(scales::hue_pal()(2)[1], 
                                scales::hue_pal()(2)[2])) + 
  geom_hline(yintercept = 0) + 
  geom_vline(xintercept = 0)
g_3